実験を繰り返すことを反復(replication)といいます。データの信頼性を向上させたいときには、同じ条件での実験を繰り返しますよね。要因実験(Factorial experiment)を用いてデータを得る際も、各実験条件を複数回繰り返すことで信頼性を向上(結果のバラつきを減少)させることができます。
でも実は、要因実験の反復を行う場合、同じ実験回数で”ついでにもう1因子”の影響を調べることができることをご存じでしょうか?
本記事では、その理由と実例を紹介していきたいと思います。
「ついでにもう1因子」を調べられる理由
最もベーシックな要因実験であるk因子2水準の要因実験は2k要因実験です。この実験計画に必要な実験回数は名前の通り2k回でした。
例えば、調べたい対象の因子が2因子の場合は22=4回、3因子の場合は23=8回、4因子の場合は24=16回…といった感じです。
要因実験の基本的な仕組みや使い方についてはこちらの記事(計画編・解析編)をご覧ください。
実験の誤差を考える場合、複数回の実験を行いますよね。このような反復を行う場合の実験回数をを考えてみましょう。
例えば、調べたい対象の因子が2因子の場合、22=4回の実験を反復する(繰り返す)場合はその2倍の回数が必要となるため、22x2=8回の実験が必要となります。3因子の場合は23x2=16回となりますね。
因子数と反復の有無による実験回数をまとめてみると次のようになります。
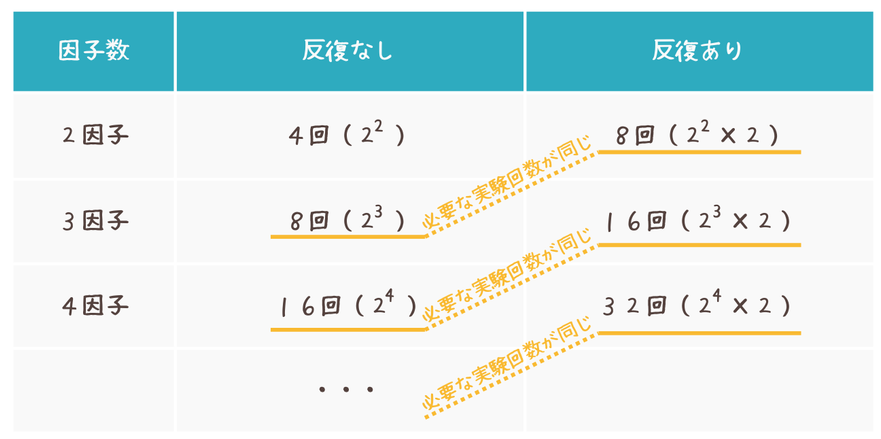
反復ありの場合に必要となる実験回数は、1因子追加した反復なしの場合に必要となる実験回数と同じになっている点がポイントです。
(たとえば、「2因子の反復あり」と「3因子の反復なし」の場合に必要な実験数は同じく8回)
これが要因実験の繰り返しを行う場合は「ついでにもう1因子」の影響を調べることができる所以です。
メリットとデメリット
「ついでにもう1因子」調べられる理屈はわかったけど、何かしらデメリットもあるんでしょ・・・?
そう感じるのは当然かと思いますので、ここで改めてメリットとデメリットをまとめておきます。
使用例
まずはメリットである「ついでにもう1因子」が調べられることを実例で確認してみましょう。交互作用が存在する例を取り上げています。
おいしいホットサンドを作るための実験を例として取り上げます。因子として、2水準の3因子を考えます。
パンの種類(A・B)、マスタードの有無(あり・なし)、焼き時間(3分・5分)
すべての組み合わせを実験し、実験を2回繰り返した結果は以下のようになりました。(全16データ)
結果はおいしさを表す架空の単位「うま」で表し、大きい方がおいしいホットサンドであることを示しています。
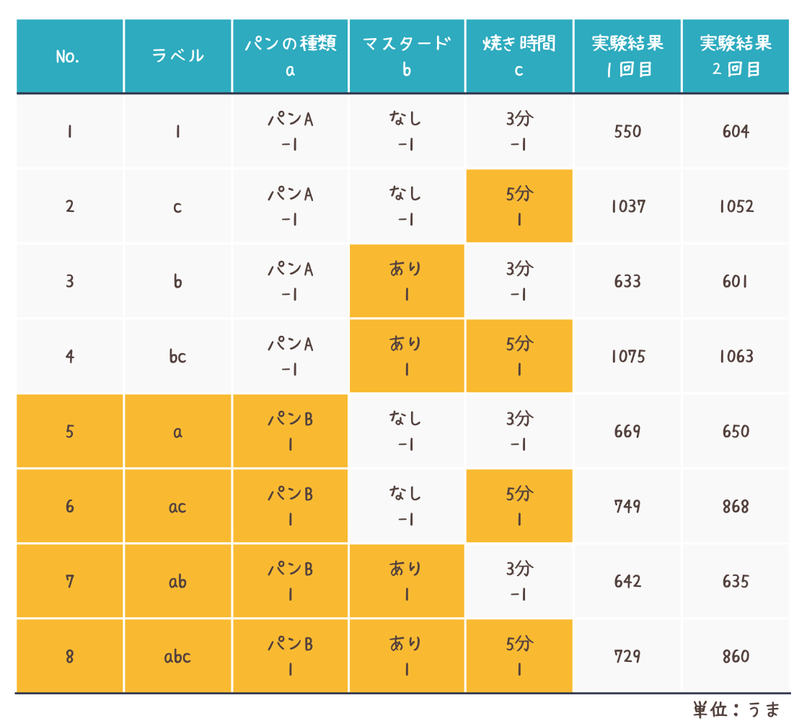
今回は上記のデータを以下の5パターンに分けて解析を行ってみます。
- 因子cが水準+1のデータのみ(8点)を用い、22要因実験(反復あり)として解析
- 因子cが水準-1のデータのみ(8点)を用い、22要因実験(反復あり)として解析
- 測定1回目のデータのみ(8点)を用い、23要因実験(反復なし)として解析
- 測定2回目のデータのみ(8点)を用い、23要因実験(反復なし)として解析
- 全データ(16点)を用い、23要因実験(反復あり)として解析
③と④の実験が今回紹介したい「ついでにもう1因子」を取り上げた実験です。
各実験計画と解析結果をまとめた表がこちらです↓
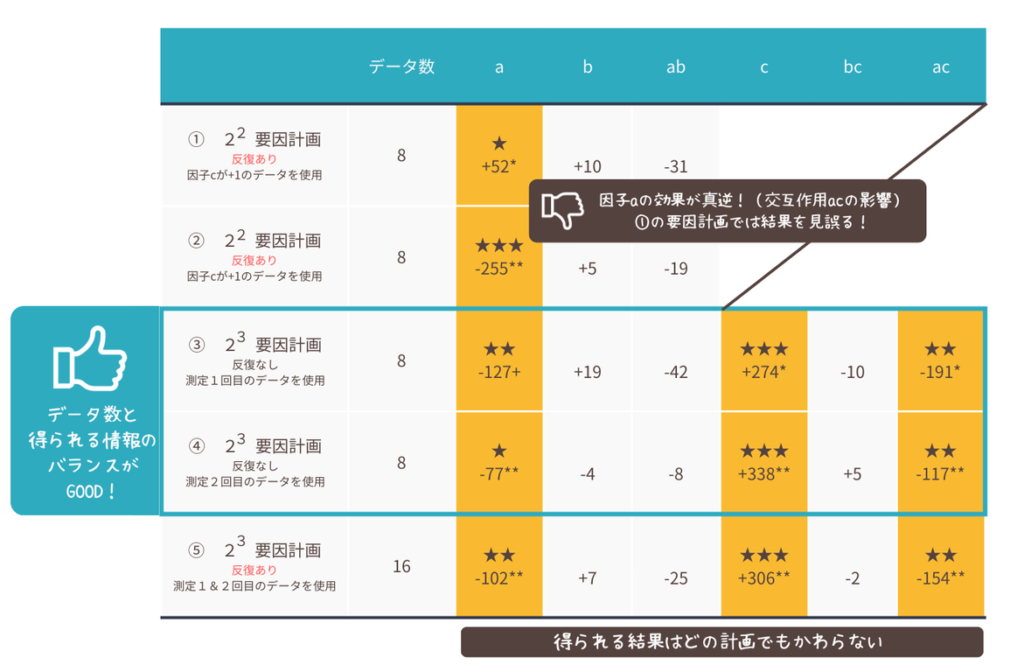
表に示した数値は効果の大きさを表しており、200以上を★★★、100以上を★★、50以上を★としています。
ここで解析結果のポイントをまとめてみましょう!(数値の右上の*については、補足をご覧ください)
以上の結果から、8回実験するリソースがある場合は23要因実験を実施するのがお得と言えそうです。同じ実験数の22要因実験と比較し、因子cと交互作用acの効果を検出することができました。
一方で22要因実験の場合は、本来存在する交互作用acの影響が考慮されないため、因子cの水準によって因子aの効果が真逆になってしまいました。むしろ22要因実験は結果を誤る可能性があると言えそうですね。
また、反復あり23要因実験(⑤))については、反復なし23要因実験(③、④)と得られる情報が同じですので、16回実験するリソースがある場合は「ついでにもう1因子」を増やし24要因実験を計画するのが好ましいと言えます。
上の例では絶対値によって効果を大きさを判断していますが、統計的にはF検定を行って誤差と効果の影響を比較する必要があります。表中の記号はF検定を行う際の有意水準を表しており、** 1%、* 5%, + 10%で有意であることを表しています。有意水準は検定を行う際の尺度で小さい値を設定して有意である場合、効果が大きいと判断されるものです。
基本的に効果が大きい(★が付いている)結果は、F検定で有意である結果(*か+)と一致していますね。F検定で客観的な判断をすることもできますが、効果の大きさから判断する主観的な方法も意外と有効です。
反復をした方がいいケース
ここまで、反復するよりも「もう1因子」を調べる方がお得な例を紹介しましたが、必ずしも反復が不要というわけではありません。
次の例に示すようにバラツキが大きいデータの場合は反復が必要です。反復を行わないと正しい判断ができなくなってしまいます。
例1と同じく、おいしいホットサンドを作るための実験を例として取り上げます。因子として、2水準の3因子を考えます。
パンの種類(A・B)、マスタードの有無(あり・なし)、焼き時間(3分・5分)
すべての組み合わせを実験し、実験を2回繰り返した結果は以下のようになりました。(全16データ)
結果はおいしさを表す架空の単位「うま」で表し、大きい方がおいしいホットサンドであることを示しています。
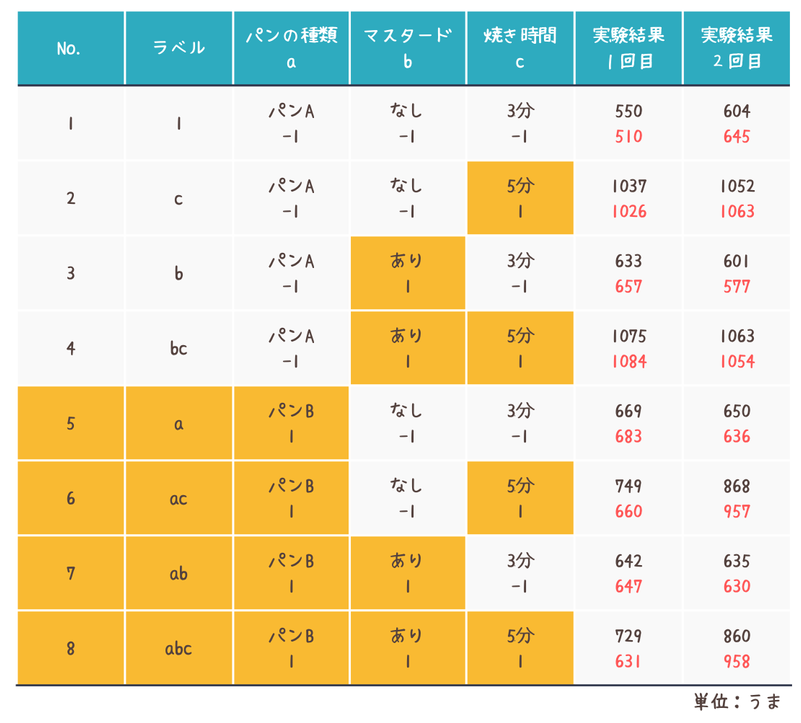
例2ではバラツキの異なる2つのデータを扱います。
- バラつき標準のデータ(黒字)
例1と同じデータ - バラツキの大きなデータ(赤字)
例1の結果と平均値との差を1.5倍したデータ。
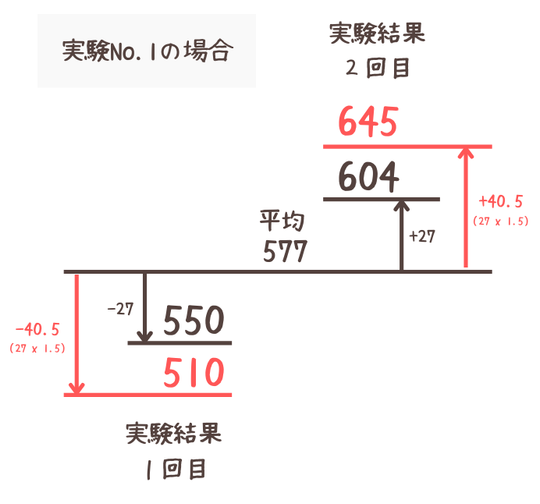
例えば、No. 1の実験結果の場合、実験1回目と2回目の結果の平均値は577であり、平均値とそれぞれの結果の差は±27です。この差を1.5倍し平均値から±40.5したデータとしています。
図で表すと以下のようなイメージです。
これらのデータをそれぞれ23要因実験として解析してみましょう。測定1回目と2回目のデータを解析の結果は以下の通りです。
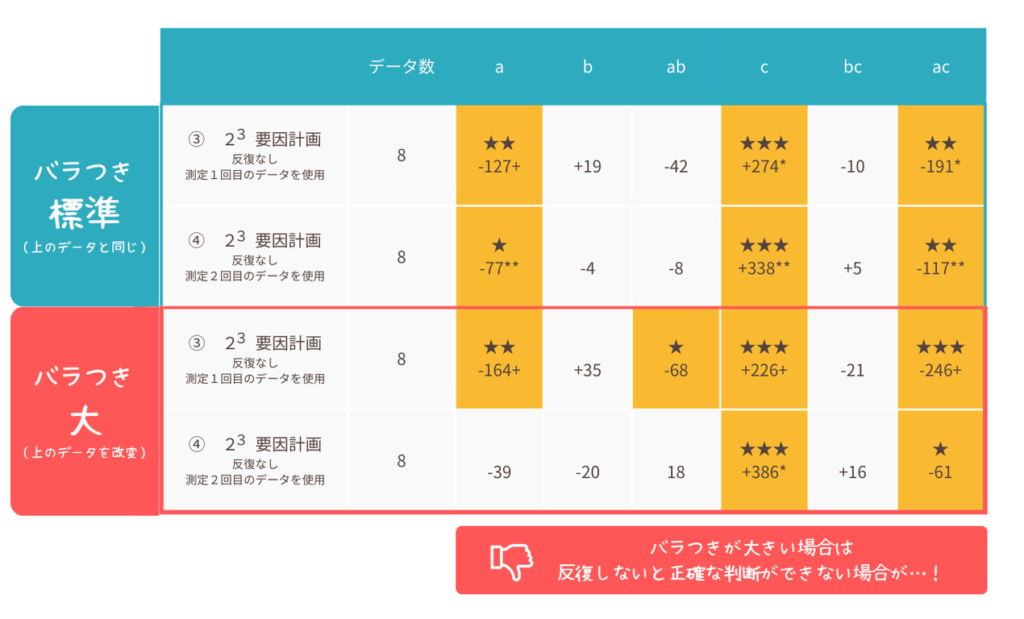
①バラつき標準のデータは例1と同じデータですので、例1と同じ解析結果が得られています。(因子a, cと交互作用acの効果が大きい)
一方、②バラツキの大きなデータでは、使用するデータで結果が異なっています。測定1回目のデータの場合は、因子a, cと交互作用acに加え、交互作用abも効果が大きくなっている一方、測定2回目のデータの場合は、因子aの効果が小さく、因子cと交互作用acのみが大きくなっています。
このようにバラツキが大きいデータの場合は、データのバラつきによって結果もまちまちです。このような場合は、後からデータを追加して反復を行えばOKですね。
まとめ
今回は要因実験で因子を増やすことのメリット・デメリットを説明しました。
「ついでにもう1因子」を調べることで、より効率的に実験を進めましょう!
更新履歴
2025/1/31 公開




コメント