実験計画法で直交表などを使うとつきまとう交絡
直交表などを使用した場合に
主効果や交互作用が混ざりあってしまう現象です
要因計画(総当たり実験)の場合は
もれなくすべての情報が手に入るわけですが…
直交表を使う場合には実験数を減らす代償として情報が混ざりあいます
この交絡関係を調べる方法はいろいろあるわけなのですが
どんな計画に対しても調べられる万能な方法があったらいいな
と思いませんか?
あるんです、これが。
積和行列を使用することで交絡関係を調べることができます
以下では直交表\(L_8\)を使用し
積和行列を使用して2水準計画の交絡関係を求める方法を説明します
交絡関係の計算方法
1. 計画行列とその拡張
実験計画を表した行列を計画行列(design matrix)と呼びます
直交表\(L_8\)の場合はこんな感じ
各列がそれぞれの主効果(A~G)に対応しています
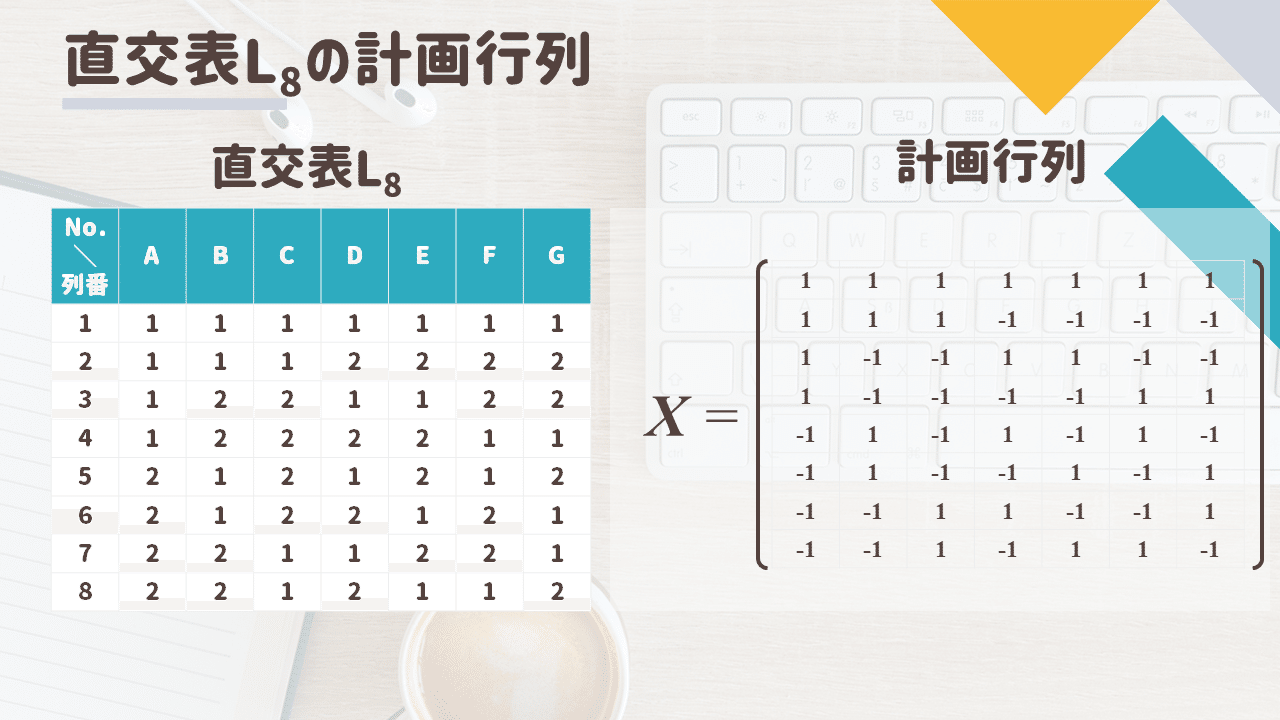
この計画行列\(\boldsymbol{X}\)に2因子間交互作用の列を加える形で拡張します
交互作用の列は元となる主効果の列の要素をかけ算する(アダマール積を計算)することで得ることができます
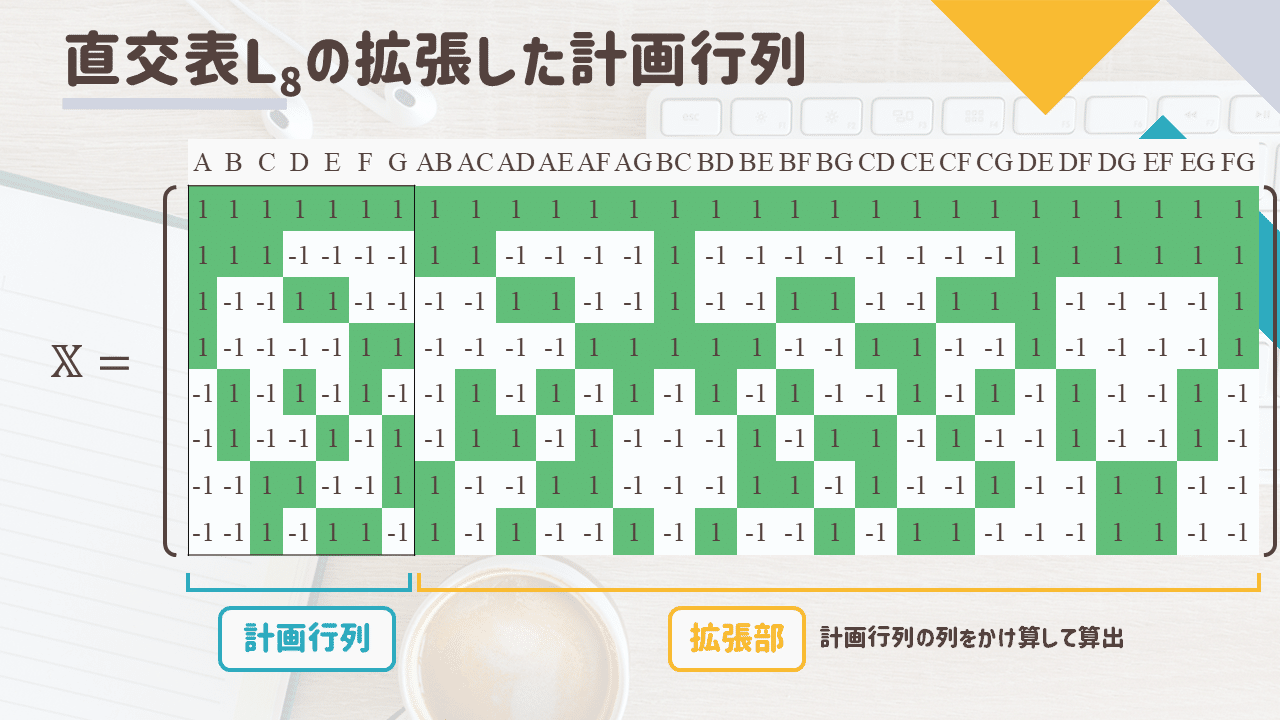
この行列には名前があるかわからないのですが
この記事では拡張した計画行列と呼び、\(\mathbb{X}\)で表すことにします
2. 拡張した積和行列
拡張した計画行列とその転置行列の積を計算することで
拡張した積和行列\(\mathbb{X}^T\mathbb{X}\)を算出します
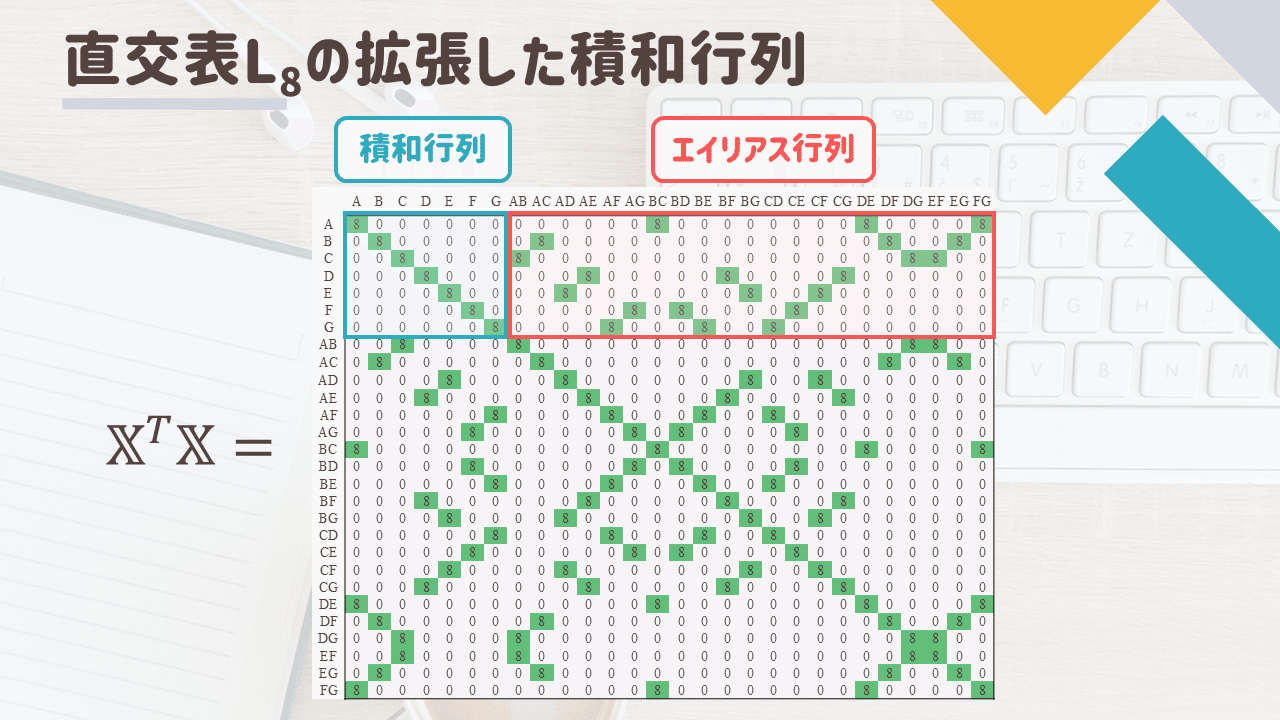
この行列は積和行列\(X^TX\)とエイリアス行列\(A\)と呼ばれる部分から構成されており
これらの中身をみることで交絡関係を調べることができます
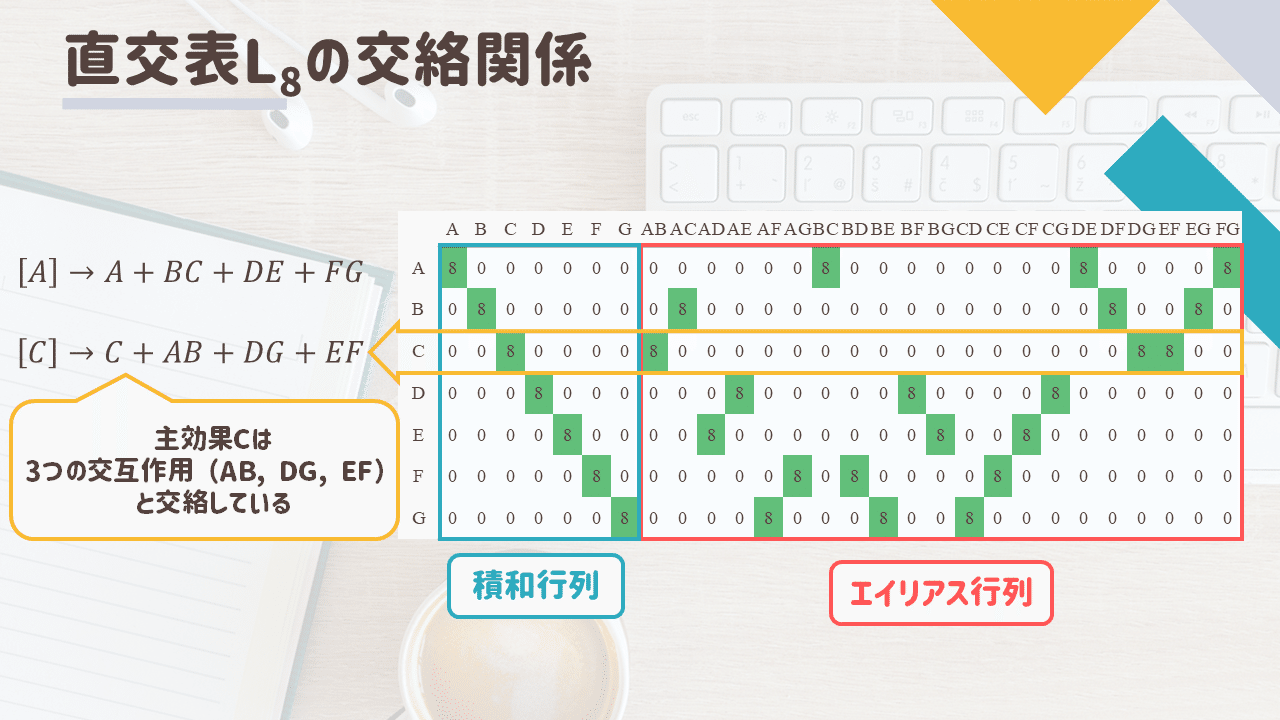
たとえば主効果Cについて考える場合は
行列の3行目を横に見ていくとC、AB、DG、EFの4列に数字が書いてあります
これはこれら4つの主効果および交互作用が交絡していることを表しています
まとめ
直交表\(L_8\)を例に拡張した計画行列から交絡関係を導く方法を紹介しました
今回紹介した方法では2水準系の計画であれば
どのような計画にも適応が可能(なはず)です
一方で3水準系や混合系の計画では
少しテクニックが必要となりますので別な記事で解説予定です
また
「なんで上の計算で交絡関係を調べるられるの?」
という疑問に対して別途説明の記事を用意しますのでご期待ください!
更新履歴
2025/10/16 noteから引越し




コメント