要因実験(Factorial experiment, Factorial design)は最も基本的な実験計画であり総当たりでデータを取得します。各要因を個別に調査していく逐次的な一因子実験などと異なり、交互作用の影響も調査できますが、必要な実験数が多いのが難点…
このページでは具体例を交えつつ、要因実験の解析方法を紹介していきます。
| 実施難易度 | ★☆☆ |
| 定義 (JISZ8101-3) | 二つ以上の水準で探求される二つ以上の因子の すべての可能な処理から構成される実験 |
| オススメのつかいかた (スクリーニング or 最適化) | 因子が多い場合のスクリーニング実験 部分要因実験との合わせを推奨 |
| メリット | 交互作用の発見が可能 |
| デメリット | 実験回数が多い |
| 必要なサンプルサイズ | 水準数の積 |
| 設定可能水準数 | 任意 |
要因実験の解析の流れ
計画編でもお伝えした通り、要因実験では2水準因子の取り扱いがオススメです。理由としては、3水準因子の場合は、要因計画ではない実験計画の方が好ましいためでした。
以上を踏まえ、解析編では2水準因子の解析方法に絞って紹介していきます。
さっそく、解析の流れをざっくりと確認しましょう。
1.実験条件をラベルに変換
今後の解析を簡単にするため、因子をアルファベット(a, b, c …)に、水準を数字(-1 or +1)に変換します。
つぎに、各実験結果にラベルを付与します。実験結果に対し、ある因子の水準が+1である場合にその因子のアルファベットをラベルとして付与します。
ラベルの付与については、言葉で説明すると分かりにくいと思いますので、今はよくわからなくとも大丈夫。使用例をみるとよくわかると思います。
2.主効果を算出
次の式を用いて主効果を算出します。
\[ 因子aの主効果 = 因子aが水準+1である結果の平均-因子aが水準-1である結果の平均\]
もしくは
\[因子aの主効果 = ラベルがaを含む結果の平均-ラベルがaを含まない結果の平均\]
ここでは因子aの主効果の算出式を記載していますが、他の因子(b, c …)の場合も同様に算出できます。
3.交互作用の効果を算出
次の式を用いて交互作用の効果を算出します。
\[因子abの交互作用 = ラベルがabを含む結果の平均-ラベルがabを含まない結果の平均\]
ここでは因子abの交互作用の算出式を記載していますが、他の交互作用(bc, ac …)の場合も同様に算出できます。
4.平均応答のグラフ化
最後に平均応答(各因子の水準ごとの平均)を算出して表やグラフに可視化して結果を確認しましょう。
主効果を確認する主効果プロットを作成ためには、各因子について水準ごとの結果を平均するだけでOKです。例えば、因子aについては以下の2つを計算しましょう。
- 因子aが水準+1である結果の平均値
- 因子aが水準-1である結果の平均値
交互作用の効果が大きい因子に関しては交互作用プロットを作成して様子を確認します。例えば、交互作用abについては以下の4つの平均を計算します。
- 因子aが水準+1のときに因子bが水準+1であるデータの平均値
- 因子aが水準+1のときに因子bが水準-1であるデータの平均値
- 因子aが水準-1のときに因子bが水準+1であるデータの平均値
- 因子aが水準-1のときに因子bが水準+1であるデータの平均値
各因子の平均応答を可視化したグラフを要因効果図とも呼びます。
これらのプロットを活用し、結果を解釈していきます。
使用例
解析の流れだけではイメージがわかなかったと思いますので、実例を紹介します。
解析を行うイメージをつかんでください!
おいしいホットサンドを作るための実験を例として取り上げます。因子として、2水準の3因子を考えます。
パンの種類(A・B)、マスタードの有無(あり・なし)、焼き時間(3分・5分)
すべての組み合わせ(2x2x2=8通り)を実験し、実験を2回繰り返した結果は以下のようになりました。
結果はおいしさを表す架空の単位「うま」で表し、大きい方がおいしいホットサンドであることを示しています。
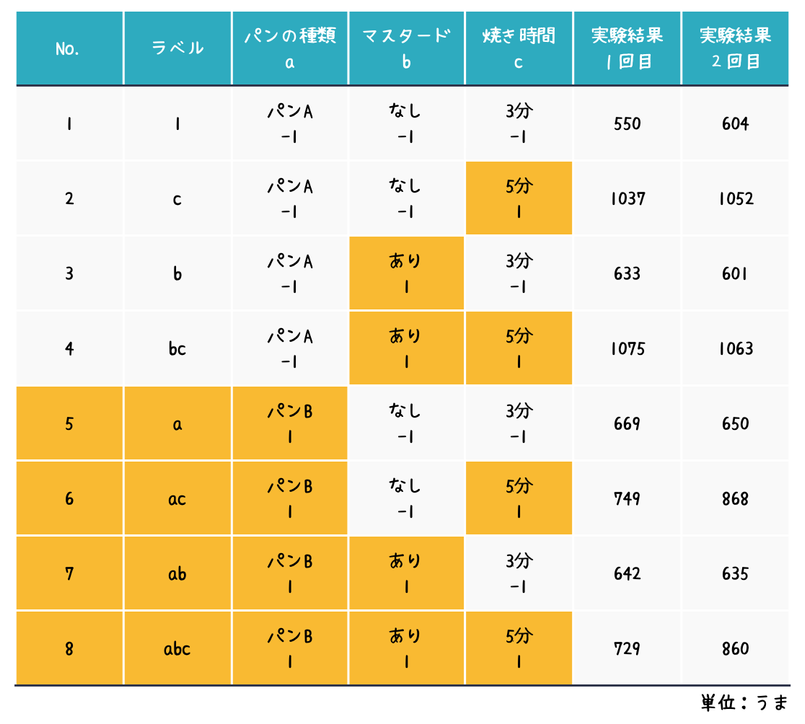
では、ここから上の手順に則って解析を進めていきましょう!
1.実験条件をラベルに変換
まずは因子をアルファベット(a, b, c …)に、水準を数字(-1 or +1)に変換します。パンの種類を因子a(パンAを-1, パンBを+1), マスタードの有無を因子b(なしを-1, ありを+1), 焼き時間を因子c(3分を-1, 5分を+1)としました。
次に各実験条件にラベルを付けます。
No. 1の条件 = 水準が+1である因子がないので、アルファベットは付与されません。便宜上、数字の「1」を付与します。
No. 2の条件 = 因子cのみ水準が+1ですので、アルファベット「c」が付与されます。
No. 3の条件 = 同様に「b」が付与されますね。
No. 4の条件 = 因子bとcの水準が+1ですので、アルファベット2文字「bc」が付与されます。
以下同様にラベルを付与していきます。
上の表にすでに記入していますので、確認してみてください。
2.主効果を算出
まずは因子a(パンの種類)の主効果を算出してみます。公式を改めて確認しておきましょう。
\[ 因子aの主効果 = 因子aが水準+1である結果の平均-因子aが水準-1である結果の平均\]
もしくは
\[因子aの主効果 = ラベルがaを含む結果の平均-ラベルがaを含まない結果の平均\]
1つ目の式の右辺第1項「因子aが水準+1である結果」はNo. 5~8の実験結果を表し、右辺第2項「因子aが水準-1である結果」はNo. 1~4の実験結果を表しています。
実は2つ目の式も同じことを言っており、右辺第1項はNo. 5~8、第2項はNo. 1~4を表しています。
以上を踏まえると、因子a(パンの種類)の主効果は以下の通り算出できます。
\[ \begin{align}
因子aの主効果 &= \frac{No. 5 + No. 6 + No. 7 + No. 8}{データ数}-\frac{No. 1 + No. 2 + No. 3 + No. 4}{データ数} \\[12pt]
&= \frac{(669 + 650) + (749 + 868) + (642 + 635) + (729 + 860) }{8}-\frac{(550 + 604) + (1037+1052) + (633+601) +(1075+1063)}{8} \\[12pt]
&= 725.25 -826.875 \\[12pt]
&= -101.625
\end{align} \]
同様に、因子b(マスタードの有無)と因子c(焼き時間)の主効果も算出してみましょう。
\[ \begin{align}
因子bの主効果 &= \frac{No. 3 + No. 4 + No. 7 + No. 8}{データ数}-\frac{No. 1 + No. 2 + No. 5 + No. 6}{データ数} \\[12pt]
&= 779.75 -772.375 \\[12pt]
&= 7.375 \\[12pt]
因子cの主効果 &= \frac{No. 2 + No. 4 + No. 6 + No. 8}{データ数}-\frac{No. 1 + No. 3 + No. 5 + No. 7}{データ数} \\[12pt]
&= 929.125-623\\[12pt]
&= 306.125
\end{align} \]
3.交互作用の効果を算出
続いて交互作用の効果を算出してみましょう。まずは因子aとbの交互作用から。公式は次の通りでした。
\[因子abの交互作用 = (ラベルがabを含む結果&ラベルがaまたはbを含まない結果の平均)-(その他の実験結果の平均)\]
改めて実験結果の表を確認すると、ラベルがabを含む結果はNo. 7, 8、ラベルがaまたはbを含まない結果はNo. 1, 2ですね。
\[ \begin{align}
abの交互作用の効果 &= \frac{No. 1 + No. 2 + No. 7 + No. 8}{データ数}-\frac{No. 3 + No. 4 + No. 5 + No. 6}{データ数} \\[12pt]
&= \frac{(550 + 604) + (1037+1052) + (642 + 635) + (729 + 860)}{8}-\frac{(633+601) +(1075+1063) + (669 + 650) + (749 + 868)}{8} \\[12pt]
&= 763.625 -788.5\\[12pt]
&= -24.825
\end{align} \]
同様に、交互作用bc, acも算出できます。
\[ \begin{align}
bcの交互作用の効果 &= \frac{No. 1 + No. 4 + No. 5 + No. 8}{データ数}-\frac{No. 2 + No. 3 + No. 6 + No. 7}{データ数} \\[12pt]
&= 775 -777.125 \\[12pt]
&= -2.125 \\[12pt]
acの交互作用の効果 &= \frac{No. 2 + No. 4 + No. 6 + No. 8}{データ数}-\frac{No. 1 + No. 3 + No. 5 + No. 7}{データ数} \\[12pt]
&= 699.25 -852.875 \\[12pt]
&= -153.625
\end{align} \]
4.効果のグラフ化
ここで、各主効果と交互作用の効果を表とグラフでまとめてみます。まずは表をつくって各効果の大きさを確認してみましょう。
各効果の大きさ(絶対値)を比較し、100以上を★★★、10以上を★★、それ以下を★と分類しました。
| 効果 | 効果推定量 | 効果の大きさ |
|---|---|---|
| 主効果a (パンの種類) | -101.625 | ★★★ |
| 主効果b (マスタードの有無) | +7.375 | ★ |
| 主効果c (焼き時間) | +306.125 | ★★★ |
| 交互作用ab | -24.825 | ★★ |
| 交互作用bc | -2.125 | ★ |
| 交互作用ac | -153.625 | ★★★ |
主効果に注目すると、主効果aと主効果cに効果がありそうです。
パンの種類や焼き時間を変更するとおいしさに影響があり、マスタードの有無はあまり影響がなさそう、ということが言えそうです。
また、交互作用acの影響が大きく、交互作用abも中程度ですが影響を及ぼしそうですね。
交互作用acが存在するということは、因子a(パンの種類)が異なる場合に、因子c(焼き時間)の効果が異なる、つまりパンの種類によっておいしく焼ける時間が異なる、と解釈できそうです。
続いて、これらをグラフ化して視覚的に確認してみましょう。まずは主効果プロットから。
因子aの効果をグラフ化する場合は、因子aが水準+1のときのデータ(No. 5, 6, 7, 8)の平均値と水準-1のときのデータ(No. 1, 2, 3, 4)の平均値をプロットすればOKです。
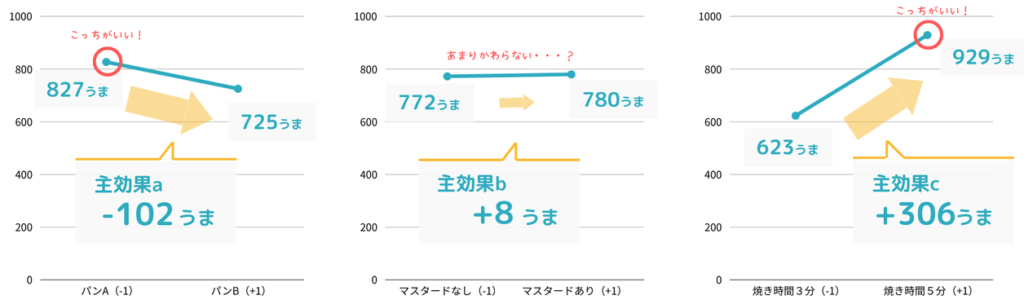
たしかに因子aと因子cを変更する場合は変化が大きく、因子bは変更してもあまり変化がありませんね。
主効果のみに着目する場合、因子a(パンの種類)は水準-1(パンA)、因子c(焼き時間)は水準+1(5分)を選択すると最もおいしいホットサンドが出来上がりそうです。
因子b(マスタードの有無)はほとんど影響がないようなので、安く・簡単に作れるように水準-1(なし)が好ましいですね。
次に交互作用を確認してみましょう。
交互作用abの効果をグラフ化する場合は、以下の4つの組み合わせをプロットすればOKです。
- 因子aが水準+1のときに因子bが水準+1であるデータ(No. 7, 8)の平均値
- 因子aが水準+1のときに因子bが水準-1であるデータ(No. 5, 6)の平均値
- 因子aが水準-1のときに因子bが水準+1であるデータ(No. 3, 4)の平均値
- 因子aが水準-1のときに因子bが水準-1であるデータ(No. 1,2)の平均値
交互作用acも同様に因子aと因子cについて4つの組み合わせを計算してプロットしましょう。
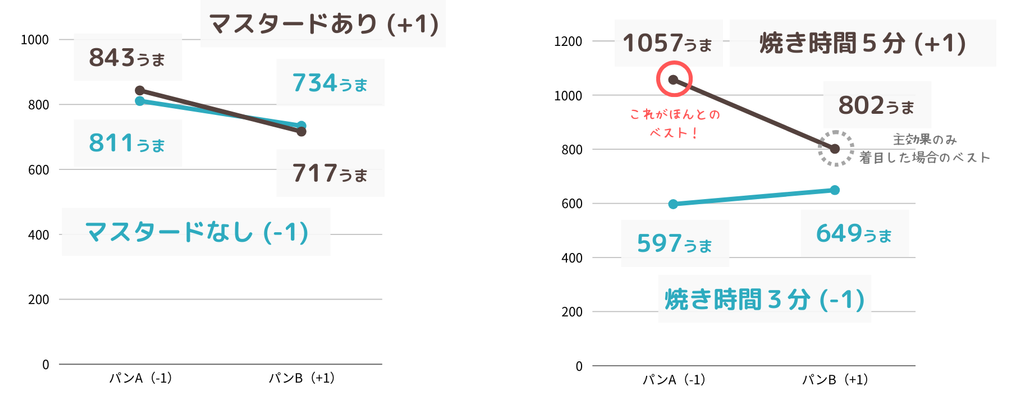
まずは左のグラフで交互作用abを確認します。
若干ではありますが因子b(マスタードの有無)がありの場合となしの場合で、因子a(パンの種類)の影響が異なっていそうですね。ただし、上の表で確認した通り影響の大きさが中程度(★★)であり、ほんの小さな差ですので、これは誤差かもしれません。因子bに関しては主効果もほとんどありませんでしたので、やはりどちらを選んでも問題なさそうです。
次に右のグラフで交互作用acを確認してみましょう。
因子c(焼き時間)が3分の場合と5分の場合で、因子a(パンの種類)の影響が異なっています。因子cが水準+1(焼き時間3分)のときは、因子aの水準+1(パンB)の方がおいしく仕上がりますが、因子cが水準-1(焼き時間5分)の場合は因子aは水準-1(パンA)の方がおいしく仕上がるようです。
交互作用を考慮すると、最もおいしいホットサンドが出来上がるのは、因子a(パンの種類)が水準+1(パンA)、因子c(焼き時間)が水準+1(5分)の場合であるといえます。
より正確に主効果や交互作用の効果の有無を判断するためには統計的検定のF検定を行う必要があります。
検定を行うことにより、効果の有無を”客観的に”判定することができます。
本記事では統計的な正確性よりも実用を重視し、数値の大小で”主観的に”判断する方法で紹介しています。
今回は2つの因子間の交互作用(2因子交互作用)を取り上げて解析を行いましたが、実は交互作用は3因子が関連する3因子交互作用も存在します。
3因子交互作用は一般的には大きく影響を及ぼさないことがわかっているため、本記事では解析を省略しました。
(実際に今回取り上げた例でも3因子交互作用はほとんど効果がありません)
まとめ
要因実験の解析方法について紹介しました。具体例を通して解析を進めるイメージがつかめてもらえればと思います。
計画編をご覧になっていない方はぜひ合わせてご確認ください!
改訂履歴
2025/1/24 公開





コメント