みなさんはどんなときに3水準以上の実験を行いますか?
おそらく因子を変更することによる変化が
直線(1次)なのか曲線(2次)なのかが知りたい場合が多いはず
このような場合は実験でデータを集めて
直線もしくは2次関数で実験データを表現したいですよね
仮に注目する因子が3つある場合は次のような回帰式の各係数 \(\beta\) を知りたいわけです
\begin{alignat*}{}
\hat y = \bar y &+ b_A x_A &+ &b_B x_B &+& x_C x_C \\
&+b_{A^2} x_A^2 &+ &b_{B^2} x_B^2 &+&b_{C^2} x_C^2 \\
&+b_{AB} x_{AB} &+ &b_{BC} x_{BC} &+& b_{CA} x_{CA}
\end{alignat*}
こんな感じの式で表したい…
このような曲線の関係性は次に示すような
3水準系の実験計画によって効率よく推定することが可能です
- 3水準系の直交表( \(L_9\), \(L_{27}\)など)
- 中心複合計画(Central composite design, CCD)
- ボックス・ベンケン計画(Box-Behnken design, BBD)
具体的には得られたデータに対して最小二乗法による回帰分析を行うわけなのですが
その際にちょっとした工夫が必要なのです
以下ではこのような問題への対応の一例として3つの因子(A, B, C)に対し
Box-Behnken計画を使用して2次モデルを最小二乗法により推定する方法をまとめました
1. 最小二乗回帰と実験計画
改めて今回の目的を整理すると
3水準の実験計画から得たデータを使用して
2次項を含む回帰式の各係数 \(\beta\)を推定することでした
この係数\(\beta\)は最小二乗法を用いることで
以下のように推定できることが知られています
\[
\hat \beta=(\boldsymbol{X}^T \boldsymbol{X})^{-1} \boldsymbol{X}^T \boldsymbol{y}
\]
ここで\(\hat \beta\)は回帰係数の推定値、\(\boldsymbol{y}\)は各データ、\(\boldsymbol{X}\)は実験の計画行列を表します
\(\beta\)の情報を得るためには
計画行列\(\boldsymbol{X}\)と各データ\(\boldsymbol{y}\)が必要なわけですね
ただし、計画行列\(\boldsymbol{X}\)は
ただ実験計画を行列にすればいいわけではありません
以下のようなちょっとした工夫が必要となります
2. 計画行列の作成
まずは基本となる実験計画を表す行列をつくります
3水準での実験を行いますので
各因子の水準を(1, 0, -1)として計画行列 \(\boldsymbol{X}\) をつくります

各列がそれぞれの因子の1次項(\(x_A, x_B, x_C\))を推定するために
使用されます
直交表を利用する場合は各水準が(1, 2, 3)になっている場合があるので
それぞれ(1, 0, -1)へ変換します
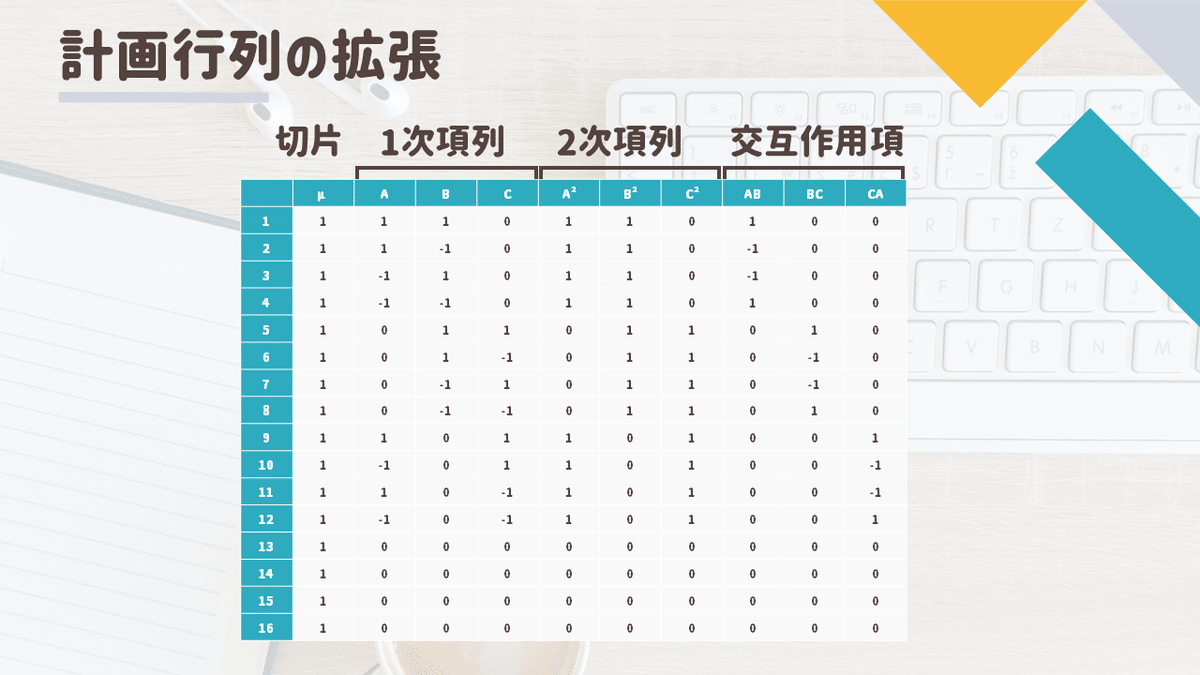
3. 計画行列の拡張
つぎに回帰分析を行うための下準備として
計画行列を拡張し列を増やします
3.1 切片
切片を推定するためすべての要素が1である列を追加します
3.2 2次項と交互作用
それぞれの因子の2次項(\(x_A^2, x_B^2, x_C^2\))と
各交互作用項(\(x_{AB}, x_{BC}, x_{CA}\))を
推定するための列を追加します
それぞれの1次項列の要素を2乗することで2次項列を生成し
2つの1次項列の要素の積(アダマール積)を計算することで
交互作用項列を生成します
2次項列、交互作用項列まで含めた行列を
ここでは拡張した計画行列と呼びます
4. 中心化
前項で作成した交互作用項列と2次項列は
更に中心化(列全体の平均値を0にする)が必要です
これによって各列が直交するようになり
回帰係数\(\hat \beta\)を推定したあとから
回帰係数を減らしても他の係数が変化しません
中心化を行ったあとの
拡張した計画行列\(\boldsymbol{X}\)と積和行列\(\boldsymbol{X}^T \boldsymbol{X}\)は
次のようになります
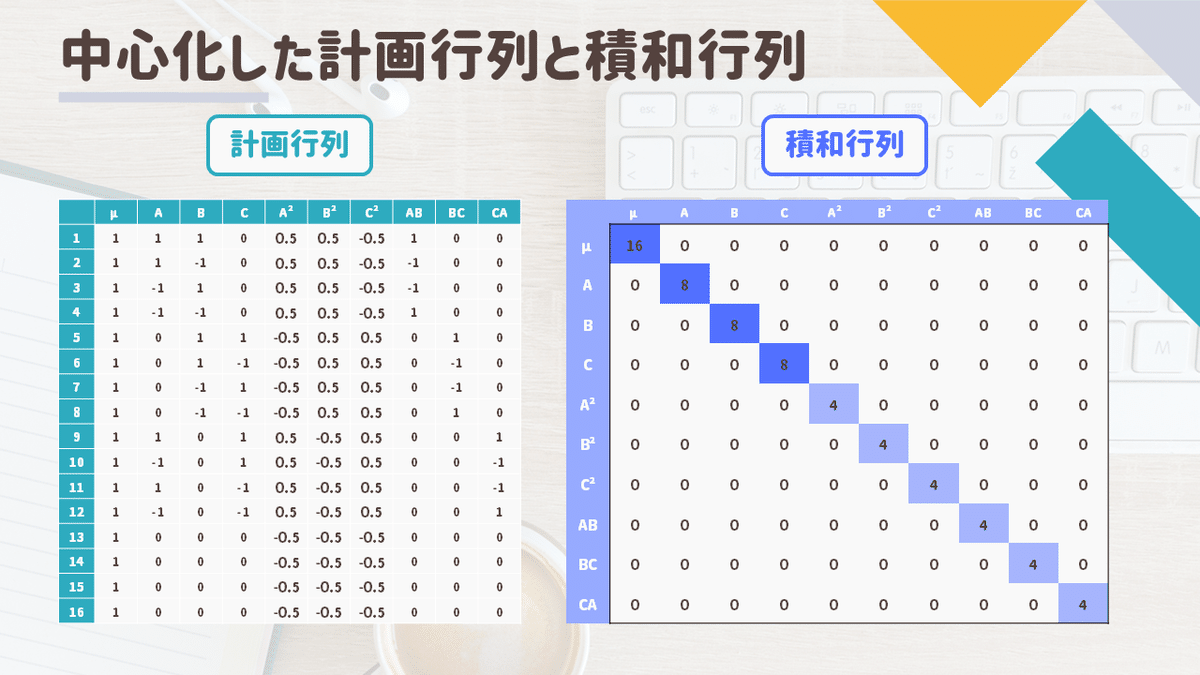
今回の例では2次項列の各値から0.5を引くことで中心化しています
各列同士の相関を表す積和行列が
対角成分を除いてキレイに0になっていますね
これで各列が直交した拡張されてた計画行列が得られましたので
いよいよ回帰分析です
5. 回帰分析
最小二乗法の式を改めて確認してみましょう
\[
\hat \beta=(\boldsymbol{X}^T \boldsymbol{X})^{-1} \boldsymbol{X}^T \boldsymbol{y}
\]
ここまで求めてきた
拡張された計画行列\(\boldsymbol{X}\)と
その実験計画で得られたデータ\(y\)を上の式に入れることで
回帰係数の推定値\(\hat \beta\)が得られるわけです
その結果以下の関係式が得られ当初の目的である実験結果を
直線、もしくは2次関数で関係性を表現できた
ことになるわけですね
まとめ
今回は3因子のボックス・ベンケン計画を例として取り上げましたが
他の3水準系計画の場合も同様の対応方法が可能です
中心化しない場合にどんな悪さがあるか
なんて話は別途記事を書きたいと思っています
更新履歴
2025/10/16 noteから引越し



コメント