直交表のしくみ

直交表を用いた実験では各因子の水準をいろいろと変更しているにもかかわらず
特定の計算を行うことで各因子の効果を他の因子の影響がない状態で算出することができます
その理由は直交表に含まれる各列が文字通り直交しているため
特定の列の効果のみを算出する場合に他の列の影響が帳消しになってしまうからです

”直交している”とは

例を通して、直交しているとはどういうことかを実際にみていきましょう
少し数式が出てきますが足し算と引き算しか行いませんので、ご安心を

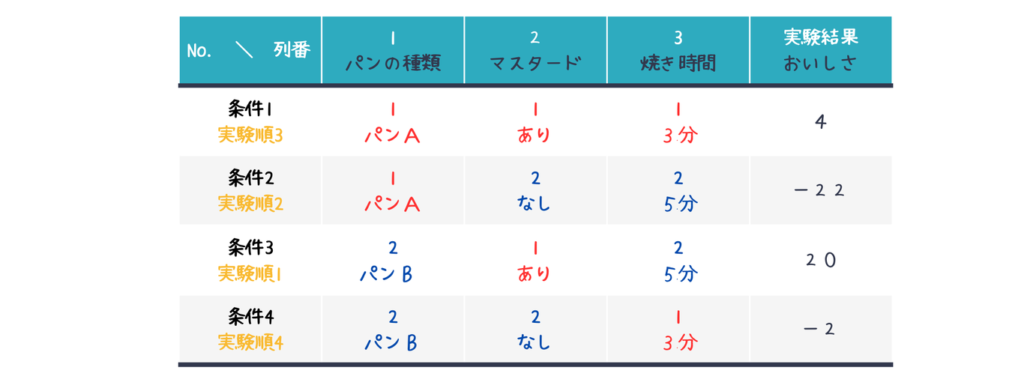
上の例の各実験データが次に示すモデルで表されると仮定します

\[y_i=\mu + \beta_1 x_{1i} + \beta_2 x_{2i} + \beta_3 x_{3i} \]

ここで\(y_i\)は\(i\)番目の実験における実験結果（この例の場合はおいしさ）
\(x_{1i}, x_{2i}, x_{3i}\)は\(i\)番目の実験における実験条件（パンの種類、焼き時間、マスタードの有無）に対応します

各実験における実験結果と実験条件を上記のモデルに代入すると以下の４つの式が得られます

\[ \begin{alignat}{3}
&\mu &+ \textcolor{#2eabbf}{\beta_1} &+ \beta_2 &+ \beta_3 &= 4 \tag{1} \\[12pt]
&\mu &+ \textcolor{#2eabbf}{\beta_1} &- \beta_2 &- \beta_3 &= -22 \tag{2} \\[12pt]
&\mu &- \textcolor{#2eabbf}{\beta_1} &+ \beta_2 &- \beta_3 &= 20 \tag{3} \\[12pt]
&\mu &- \textcolor{#2eabbf}{\beta_1} &- \beta_2 &+ \beta_3 &= -2 \tag{4}
\end{alignat} \]

ただし、\(x_{1i}, x_{2i}, x_{3i}\)には直交表の各行における条件（1 もしくは 2）を1 もしくは-1として代入しています

これらの式を組み合わせて因子の効果を以下のように計算することができます

\[ 因子の効果=\textcolor{#FF3131}{\frac{水準１で実験したデータの和}{水準１で実験したデータ数\times2}}-\textcolor{#004AAD}{\frac{水準２で実験したデータの和}{水準２で実験したデータ数\times2}} \]

例えば、上記の例で\(x_1\)（パンの種類）の効果\(\beta_1\)を計算してみましょう
水準1で実験したデータは式(1)と(2)、水準2で実験したデータは式(3), (4)に対応します

\[ \begin{align}
&\frac{式(1) +式(2)}{2 \times 2} – \frac{式(3) + 式(4)}{2 \times 2} \\[12pt]
&= \frac{(\mu + \textcolor{#2eabbf}{\beta_1} + \beta_2 + \beta_3) + (\mu + \textcolor{#2eabbf}{\beta_1} – \beta_2 – \beta_3)}{4}-\frac{(\mu – \textcolor{#2eabbf}{\beta_1} + \beta_2 – \beta_3)+(\mu – \textcolor{#2eabbf}{\beta_1} – \beta_2 + \beta_3 )}{4} \\[12pt]
&=\frac{2\mu+2\textcolor{#2eabbf}{\beta_1}}{4} – \frac{2\mu+2\textcolor{#2eabbf}{\beta_1}}{4} = \frac{4\textcolor{#2eabbf}{\beta_1}}{4} = \textcolor{#2eabbf}{\beta_1}
\end{align} \]

\(\beta_1\)以外がきれいに消えてなくなっており
\(x_1\)（パンの種類）の効果\(\beta_1\)が他の実験条件の影響を受けずに計算できていることがわかります

\(x_2, x_3\)についても同様に計算することができ
それぞれ\(\beta_2, \beta_3\)以外が消えてなくなってしまいます

このように直交表は特定の実験条件（列）の効果のみを計算する際に
他の列の影響が帳消しになってしまうような実験条件で構成されています
今回の例ではL₄直交表を取り上げましたがこの性質はどんな直交表においても成り立ちます

改訂履歴

2024/12/28　公開