直交表のつかいかた

直交表はスクリーニング実験を行う際に大幅に実験数を削減できる強力なツールです
この記事では直交表の使い方を例を交えながら以下の流れで紹介します

Contents

直交表のえらびかた

直交表を選ぶために、まずは実験回数、因子数、水準数を決める必要があります

実験回数

実験回数が多い場合、たくさんの因子を調べることができますが
その一方で実験を終えるまで時間がかかります
直交表を使った実験では最後まで実験を行わないと結果がわからないため
情報量と時間のバランスから選択する必要があります

因子数

実験で調べたい因子の数を決めます
例：温度、圧力、材料の種類

水準数

実験で調べたい因子の水準数を決めます
基本的に２水準もしくは３水準とし、すべての因子に関して水準数を揃える必要があります

以上の情報から直交表一覧を参考に使用する直交表を決めましょう
上の情報とぴったり一致する直交表が存在しない場合が多いと思いますので最も近しいものを選択します

例

おいしいホットサンドを作るために直交表を使った実験を計画します
調べたい因子と水準は、パンの種類（A、B）、焼き時間（３分、５分）、マスタードの有無（あり、なし）とします
平日の朝に毎日実験をし、５日間で調べることとしました

実験回数：５回
因子数：３因子
水準数：２水準

総当たり実験を行う場合は\(2^3=8\)回の実験が必要となり
平日の間に調べきることができません

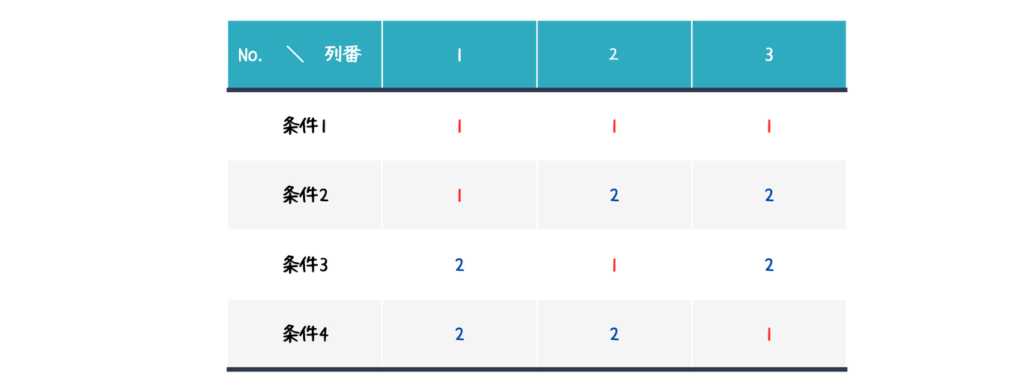
直交表一覧の２水準直交表に３因子が割り付けられるL₄ (2³)があったのでこれを使いましょう
L₄は必要な実験回数が４回なので目標とする期間内にデータがすべて集まりそうです

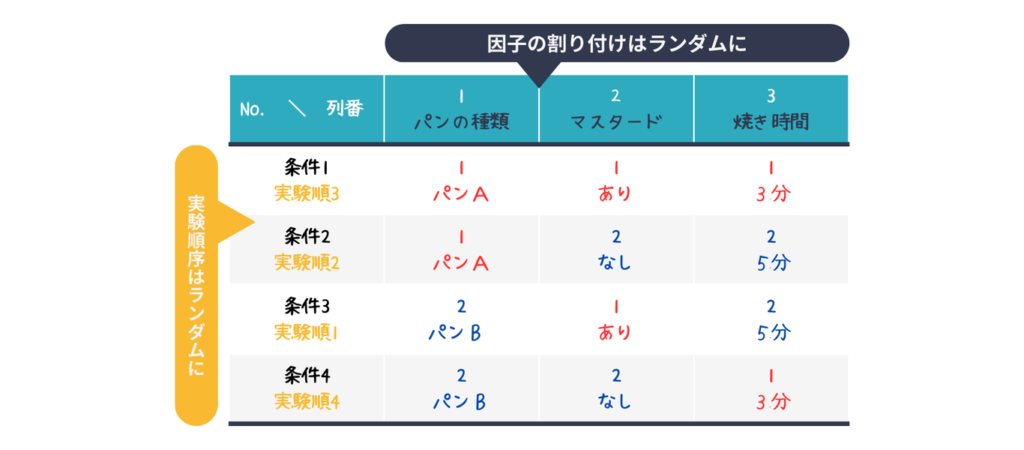
直交表を選んだら次は割付けです
直交表の各列に調べたい因子をランダムに割り付けていきます

表の中の数字（１or２）は各因子の水準を表しています
こちらもランダムに割り付けます

例

おいしいホットサンドを作るためにL₄ (2³)直交表を使うことにしました
調べたい各因子・水準を各列に割付けます

割り付けが終わった直交表の条件に従って実験を行いデータを取得していきます
データを取得する順番もランダムに決定します

得られたデータは以下の式に従って計算を行い、各因子の効果を算出しましょう

\[ 因子の効果=\textcolor{#FF3131}{\frac{水準１で実験したデータの和}{水準１で実験したデータ数\times2}}-\textcolor{#004AAD}{\frac{水準２で実験したデータの和}{水準２で実験したデータ数\times2}} \]

例

おいしいホットサンドを作るためにL₄ (2³)直交表をつかって以下の通り実験を行いデータを取得しました
数値が大きいほどおいしいホットサンドだとします

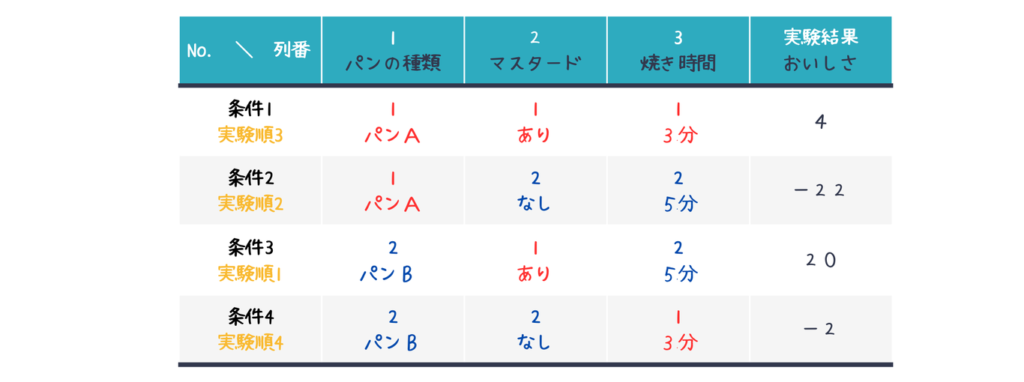
各因子の効果を計算すると以下の通りになります

おいしいホットサンドを作る（数値を大きくする）ためには
パンの種類をB、マスタードありとするとよいことがわかりました
焼き時間はあまり影響がないようです

補足

焼き時間の影響は＋１ですので、焼き時間は３分の方が若干おいしくなる可能性がありますが
測定のばらつきの可能性もあります
ばらつきの範囲かどうかを調べるためには分散分析を行う必要があります
分散分析を行う場合には因子を割り付けない列（誤差を調べる列）をつくる必要があります

注意点

直交表は上で述べた通り非常に便利なツールですが以下のようなデメリットも存在します

直交表のつかいかたをできるだけシンプルにまとめてみました

上の注意点にまとめた通り直交表は、いつでも使える便利なツール、というわけではないのですが
使いようによっては非常に強力なツールであることがおわかりいただけたのではないでしょうか

2024/12/20　投稿