実験をやるからには効率よくデータを集めたいですよね。やってはいけない、でもやってしまいがちな実験方法をまとめました。
- 総当たり実験・勘と経験頼み・1因子ごとの調査は、やめよう!
- 直交表を用いた部分要因実験など、実験計画法を使おう!
直交表の使い方はこちらの記事をご覧ください↓(むしろこっちを見て)
やってはいけない その1.総当たり実験
想定しうるすべての組み合わせを検討する方法です。力業ですべてのデータを集めればよいので、単純だけど労力がかかりますね…
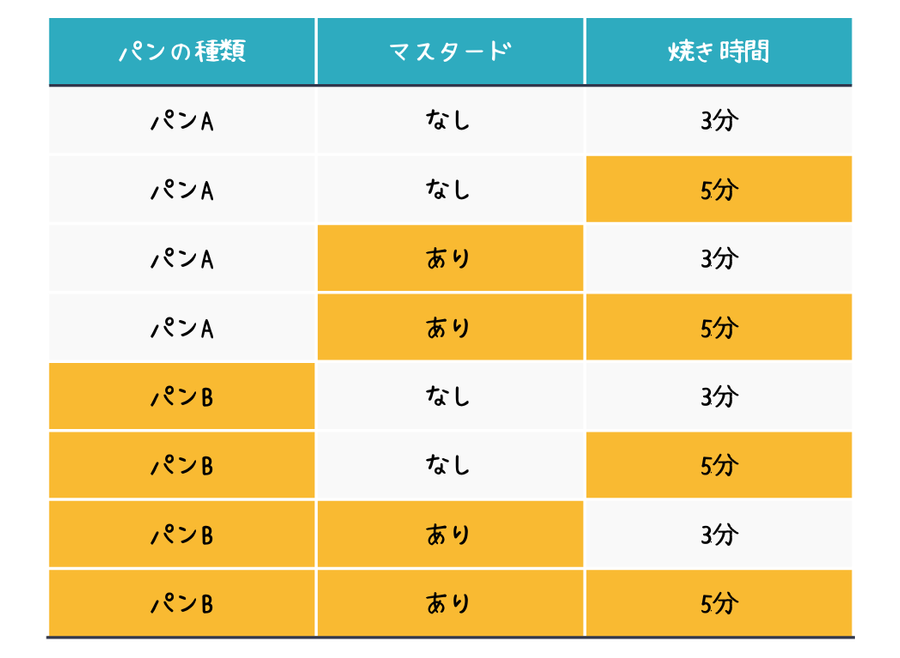
やってはいけない実験の例を示すために、おいしいホットサンドを作るための実験を例として取り上げます。因子として、2水準の3因子を考えます。
パンの種類(A・B)、マスタードの有無(あり・なし)、焼き時間(3分、5分)
総当たり実験ではすべての組み合わせ(8通り)を実験します。
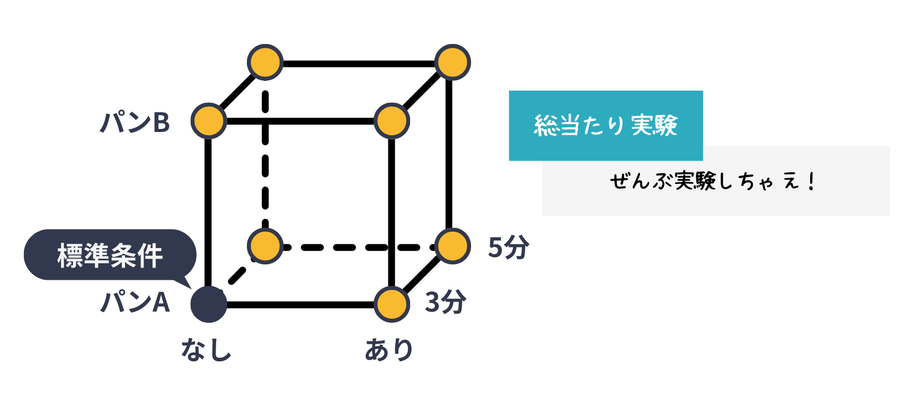
立方体の図の見方を説明します。(なんとなく分かる方は読み飛ばしてOK)
立方体の各点は実験条件の3次元プロットを表しています。
具体的には、標準条件と吹き出しが付いている左下の点=パンA・マスタードなし・焼き時間3分の組み合わせです。
標準条件から移動した点は各因子の条件が変化します。(↑に移動=パンB、→に移動=マスタードあり、↗に移動した=焼き時間5分)
例えば、標準条件の→の黄色い点はパンA・マスタードあり・焼き時間3分、標準条件の対角の黄色い点はパンB・マスタードあり・焼き時間5分を表しています。
- 因子が増えれば増えるほど実験回数が増えていく…!
やってはいけない その2.勘と経験(Best-guess approach)
勘と経験を頼りに探索する方法です。最良推定法と呼ばれることもあるようです。ある程度、その分野での経験がある方がやりがちなアプローチな気がします。
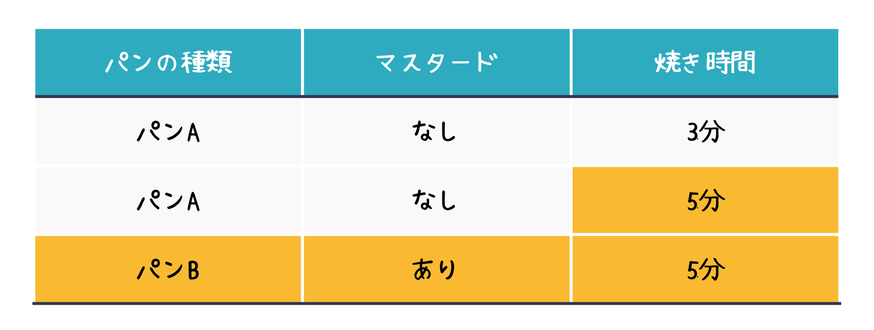
- これまでの経験を元に焼き時間の影響が大きそうだと”思った”ので、焼き時間を変更
- マスタードありにする場合は、パンBの方がおいしい”気がする”ので、マスタードありにすると同時にパンをBに変更
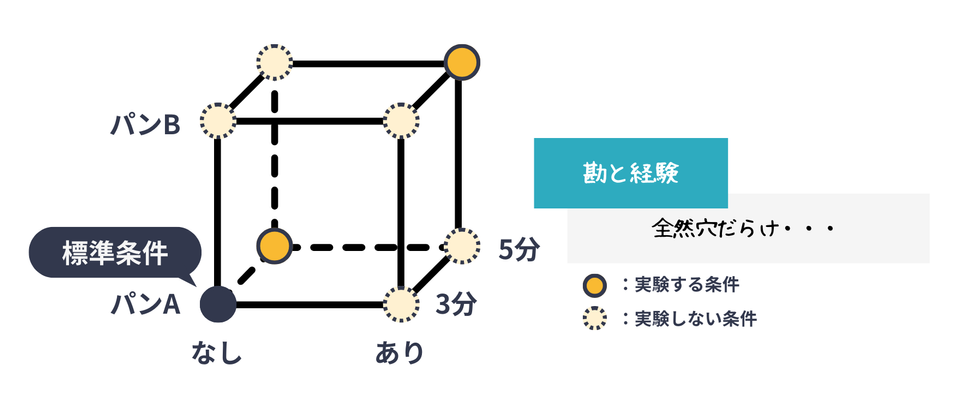
- ベストな結果が得られるまで時間がかかる&たどり着ける保証がない
- そこそこいい結果が得られたときに、それがベストな結果である保証がない
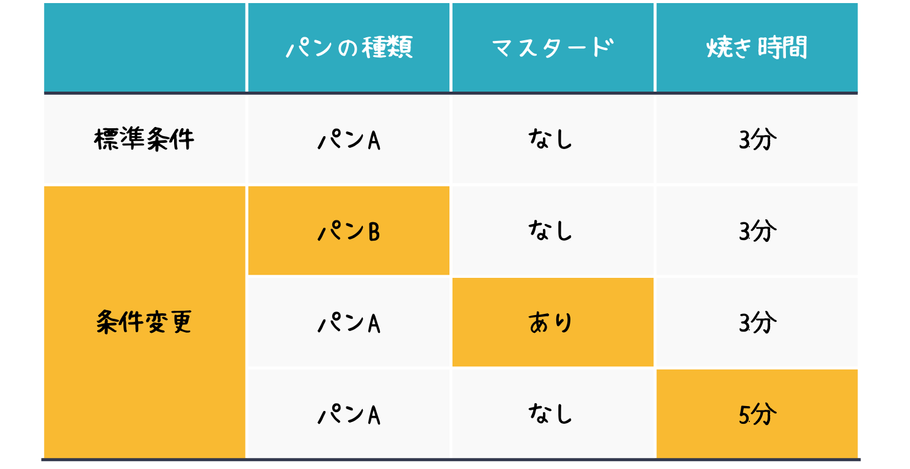
やってはいけない その3.1因子ごとの調査(One-factor-at-a-time)
標準条件を設定した上で、各因子の条件を順次変更していく方法です。なんとなく網羅的に実験できている感覚に陥るので、最も危険!下の例に示すように、実は穴だらけのプランなのです。
まずはパンの種類を変更、次にマスタードをありに変更、最後に焼き時間を変更して各影響を調査
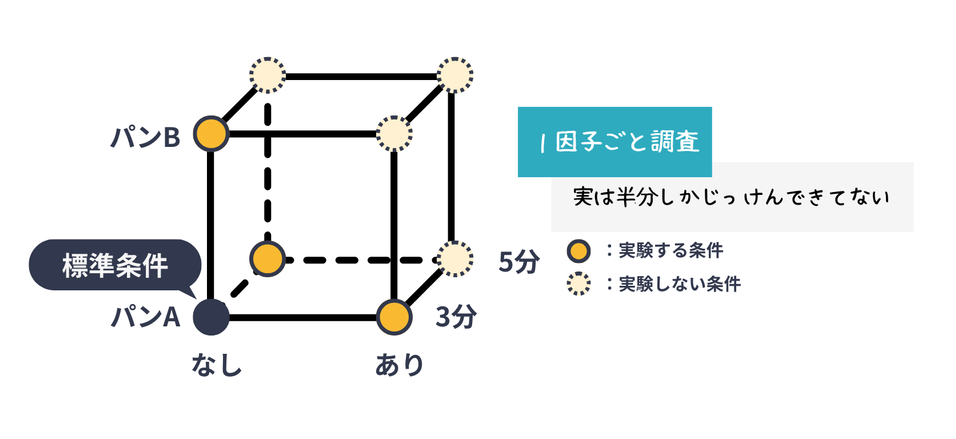
例えば、パンの種類Bとマスタードありの組み合わせがとてもおいしい!という場合に(交互作用があると言います)、その影響を確認することができなくなってしまいます。
- 交互作用が考慮されない
やるべきアプローチ 部分要因実験(直交表)
じゃあどうやって実験するべきなのか、というと、部分要因実験を使いましょう。
部分要因実験では各因子から均等に情報を得ることができるように設計されています。立方体の図を見ると、各因子の条件が均等に表れていることがわかるかと思います。
因子を割付けたL4直交表は以下の通りです。
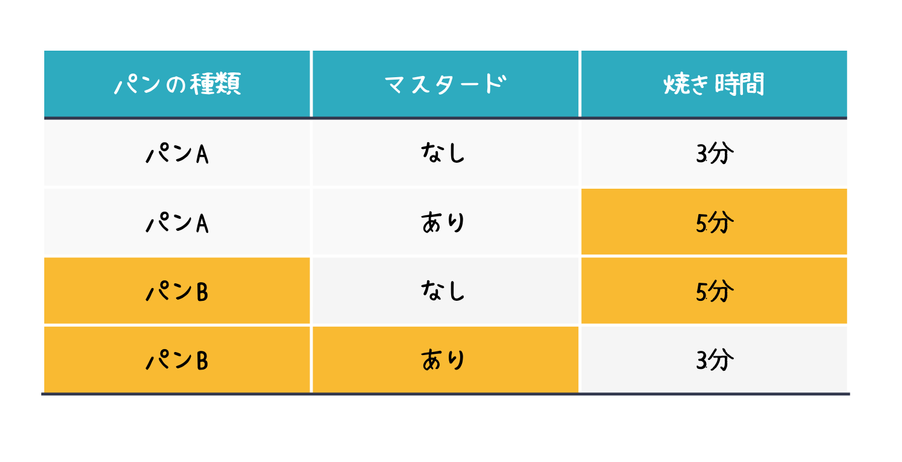
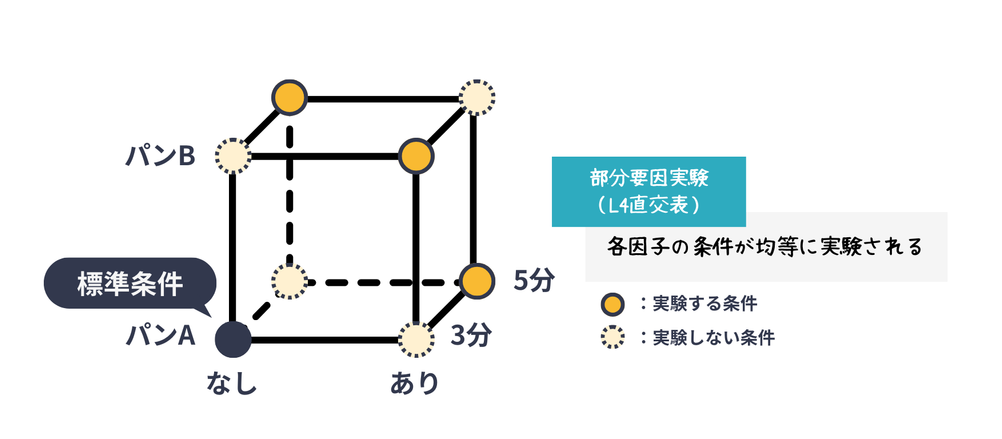
- 各因子の条件が均等に実験されるので、均等に情報を得ることができる!
まとめ
やってはいけない実験方法をまとめてみました。
- 総当たり実験 ⇒ 単純だけど労力がかかる
- 勘と経験 ⇒ その分野での経験がある方がやりがち
- 1因子ごと ⇒ なんとなく網羅的に実験できている感覚に陥る
結論を急ぐあまり見切り発車してしまうと、どうしてもこれらのようなアプローチを選択してしまいがちです。
また、そもそも部分要因実験(直交表)を知らないことには活用ですよね。ぜひ、他の記事も参考にして実験計画法を使いこなし、効率的にデータを集めていきましょう!
改訂履歴
2025/1/10 公開





コメント