実験計画法や分散分析の勉強をしたことがある方は
「実験の繰返しをしないと交互作用の情報が得られない」
このように覚えているのではないでしょうか?
私もそうでした
たとえば、よく参考にする本には以下のように書かれています
繰返しがある場合には因子数と同じ次数までの交互作用が求まり、
谷津(1991)すぐに役立つ実験の計画と解析[基礎編]
繰返しがない場合には(因子数-1)の次数までの交互作用が求まる
ところが最近
この主張には一部誤りがあるのではないか?
と思い始め、検討をおこないました
結論を先に書いてしまうと以下の通りです
繰返しがある場合:因子数と同じ次数までの交互作用を\(F\)検定できる
繰返しがない場合:(因子数-1)の次数までの交互作用を\(F\)検定できる
\(F\)検定にこだわらなければ、交互作用の情報は得られる!
以下では上記結論に至った過程を記載していきます
実験計画法=分散分析というイメージが強いのですが
他の分析方法を使うこともできるよ!
という点をアピールしつつ書いてみました
1. 配置実験≠分散分析
実験計画法を勉強すると最初にであう実験計画は配置実験
要因計画(Factorial design)とも呼ばれますね
要は総当たり実験ですね
二元配置(\(2^2\)要因計画)の場合はこんな感じ
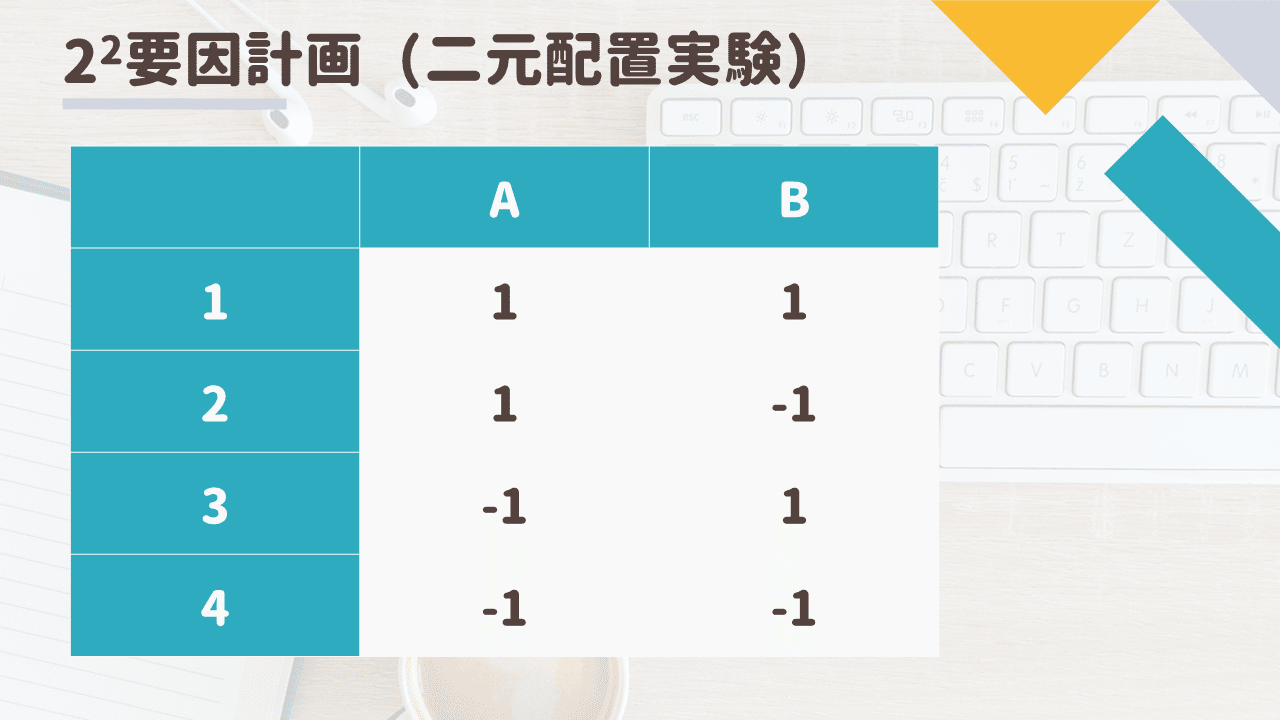
これに分散分析を組合せて
統計的に有意かどうかを\(F\)検定で判断する
というのが一般的な流れです
実験計画法の教科書は基本的にこのパターンなので
「要因計画=分散分析」というイメージが強いのですが
他の分析方法だってある!わけです
2. 要因効果図と回帰分析という選択肢
2.1. 要因効果図
各因子について各水準の平均応答をプロットしたものです
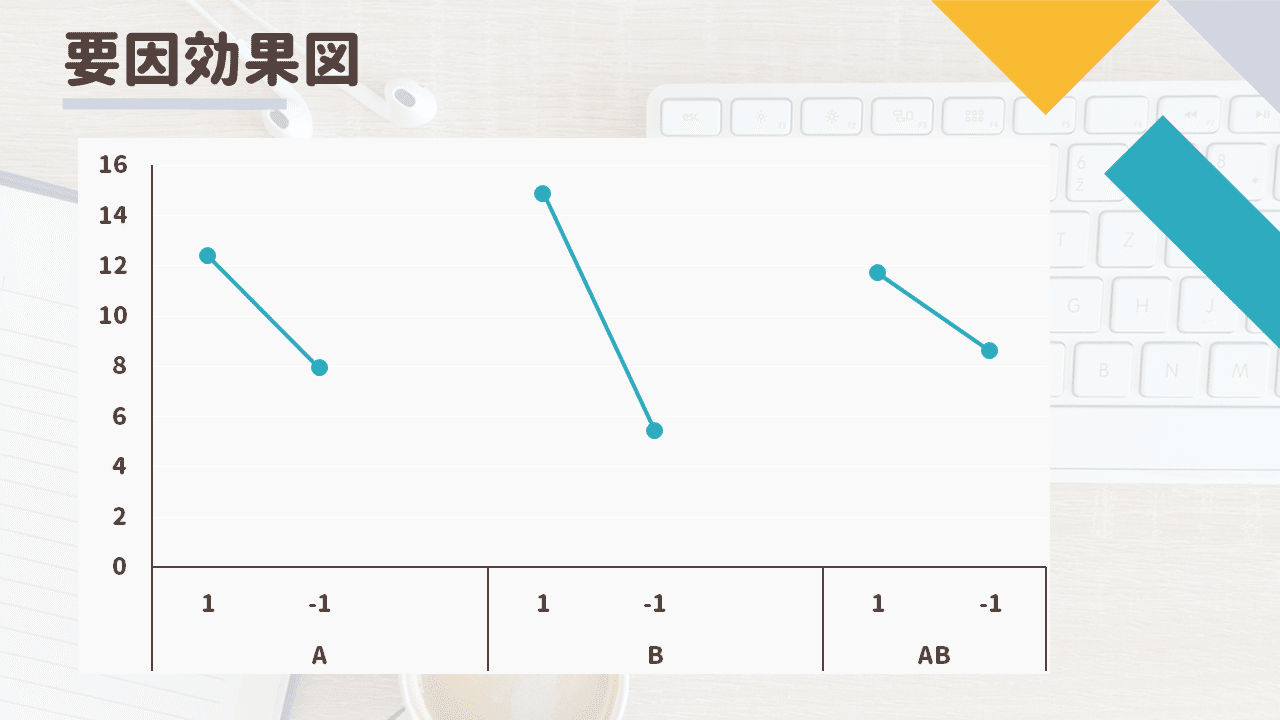
傾きが大きければ効果あり、小さければ効果なしと主観的に判断します
交互作用ABの傾きから交互作用の情報が得られそうですよね
2.2 回帰分析
モデルを想定して回帰係数を求める方法です
例えば、2水準の因子が2つある\(2^2\)要因計画(二元配置実験)では以下のような回帰モデルを想定します
\[
y = \beta_0 + \beta_Ax_A + \beta_B x _B + \beta_{AB} x_{AB}
\]
ここで\(y\)は応答、\(\beta_i\)は回帰係数、\(x_i\)は各因子の水準(1 or -1)です
二元配置実験では4回の実験を行いますので
4つの未知数\(\beta_i\)に対して式が4本得られます
\begin{alignat*}{}
y_1 &= \beta_0 + \beta_A + \beta_B + \beta_{AB} \\
y_2 &= \beta_0 + \beta_A – \beta_B – \beta_{AB} \\
y_3 &= \beta_0 – \beta_A + \beta_B – \beta_{AB} \\
y_4 &= \beta_0 – \beta_A – \beta_B + \beta_{AB}
\end{alignat*}
未知数の数と式の本数が一致しているので
この連立方程式を解けば各\(\beta_i\)が得られるわけです
回帰係数\(\beta_{AB}\)から交互作用の情報が得られそうですよね
ちなみに、上記は2因子の場合で説明しましたが
要因計画では因子数にかかわらず実験数と未知数が一致しますので
2因子以上の場合でもすべての回帰係数が求まります
詳しくはこちらの記事↓
3. \(2^2\)要因計画の実例
上記のように他の分析方法をみてみると
「え、繰返ししなくても交互作用の情報が得られそう…」
と思いませんか?
というわけで、実際のデータで検証してみました
3.1 データの設定
ここでは仮に2つの因子A、Bに対し、以下の関係が成り立つと仮定します
\[
y=10+2x_A+5x_B+x_{AB}+\varepsilon
\]
\(x_A\)は因子Aの水準(1 or -1)、\(x_B\)は因子Bの水準(1 or -1)、\(x_{AB}\)は因子Aと因子Bの交互作用、\(\varepsilon\)は-1~1の間を取るランダム誤差を表します
ランダム誤差を含めて以下のデータが得られたとします
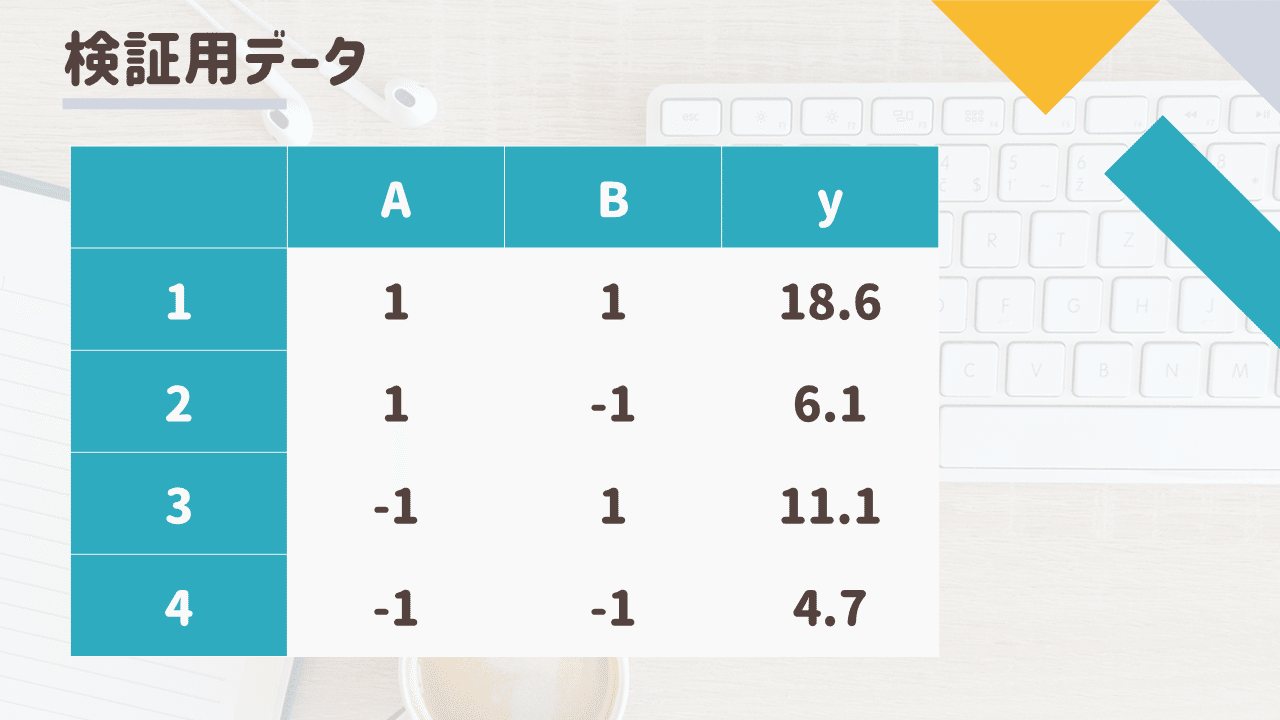
上記のように設定を行う場合、各因子と交互作用の効果は誤差の大きさ(±1)に対して以下のような関係となります
因子Aの主効果:2倍
因子Bの主効果:5倍
交互作用AB:1倍(誤差と同程度)
上記の仮定のもと繰返しのない\(2^2\)要因計画(2元配置実験)の4回の実験で得られたデータに対して
それぞれの分析方法で得られる情報を比較してみます
3.2 分散分析
繰返しを行っていない2元配置実験ですので
交互作用ABを\(F\)検定することはできません
以下の通り、交互作用ABに割り当てられる自由が足りないからです
全自由度:3 = 因子A:1 + 因子B:1 + 誤差:1
したがって分散分析表は次のようになります
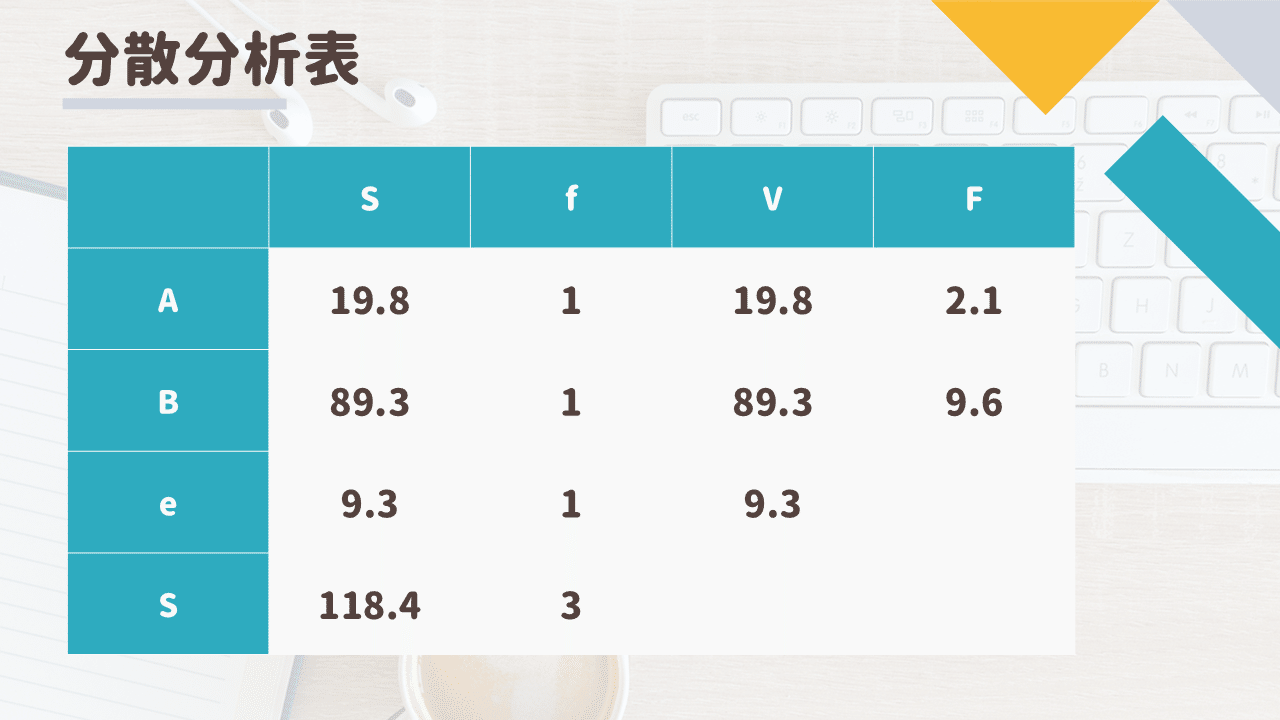
詳細は省きますが誤差の自由度が小さいので
因子Aと因子Bの主効果は有意ではなく、交互作用ABについてはもよくわからない
という結論になります
3.3 要因効果図
各因子の平均応答を算出してプロットすればOKです
交互作用については少し工夫が必要で
因子Aと因子Bの水準が同じ場合は1、異なる場合は-1 として計算します
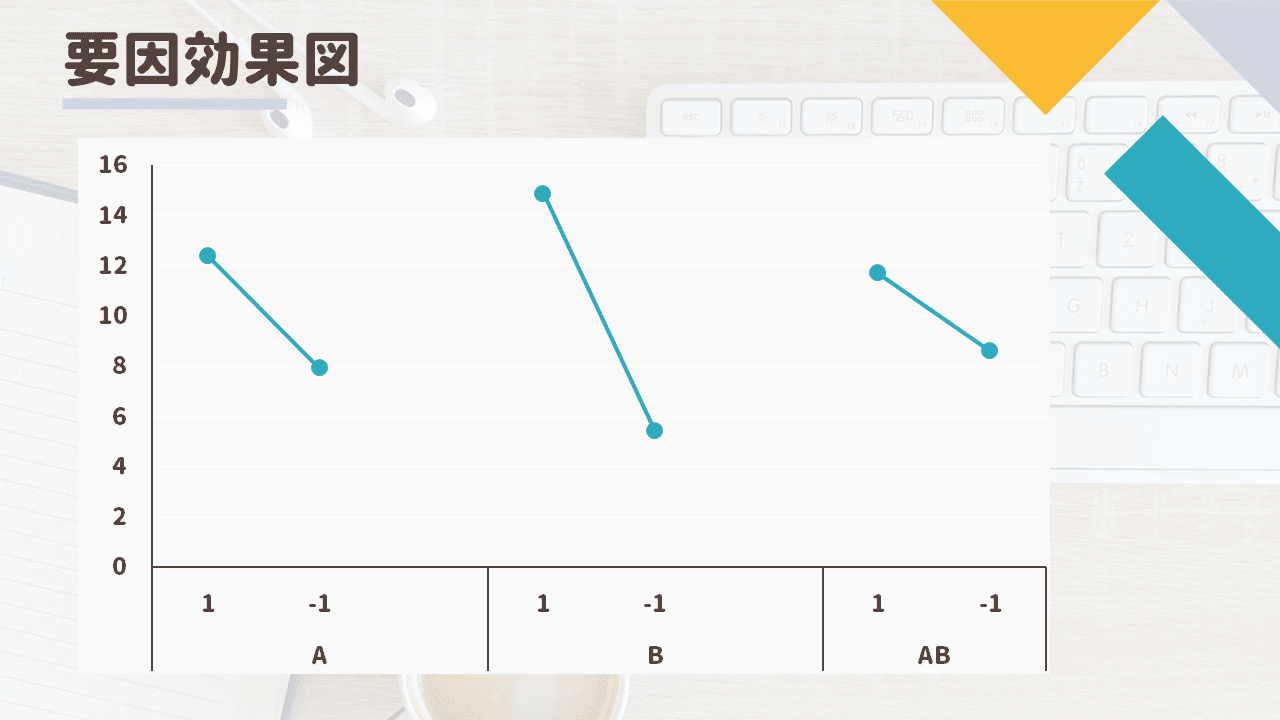
交互作用ABの傾きは因子Aと因子Bの主効果に対して小さいため
交互作用は大きくなさそう、という主観的な判断は可能です
3.4 回帰分析
上記の説明のように4つの式から4つの回帰係数を算出します

交互作用ABの係数は因子Aと因子Bの主効果の係数に対して小さいため
交互作用は大きくなさそう、という主観的な判断は可能ですね
ただし、誤差に割り当てる自由度がないため
\(F\)検定による客観的な判断はできません
4. まとめ
冒頭に述べた結論を再掲します
繰返しがある場合:因子数と同じ次数までの交互作用を\(F\)検定できる
繰返しがない場合:(因子数-1)の次数までの交互作用を\(F\)検定できる
\(F\)検定にこだわらなければ、交互作用の情報は得られる!
\(F\)検定をしようとしなければ交互作用の情報は得られるわけです
ただし、誤差の情報がないため
誤差に対する効果の大きさについては別途検討が必要です
配置実験=分散分析というイメージにとらわれてしまうと
なんだかもったいない気がしますよね
更新履歴
2025/10/16 noteから引越し





コメント